Hypothesis tests pt 4

Lecture 16

Aidan Combs

Duke University
SOCIOL 333 - Summer Term 1 2023

2023-06-14

Logistics

Introducing George

Grades are up to date
- Feedback in GitHub (issues on component 2 repo), grades on Sakai
- Check your feedback—you’ll revise what you did and use it in the final paper
- Extra credit will be added up and factored in at the end

Project component 3, results: draft by tomorrow (June 15), submit for grading by next Tuesday (June 20)
- Instructions and example are on the website
- Drafts should be complete–meaning you attempted all parts
- Commit your changes and push to GitHub!

Today

A note on bar charts for proportions
Review yesterday’s exercise
Specifics of particular hypothesis tests

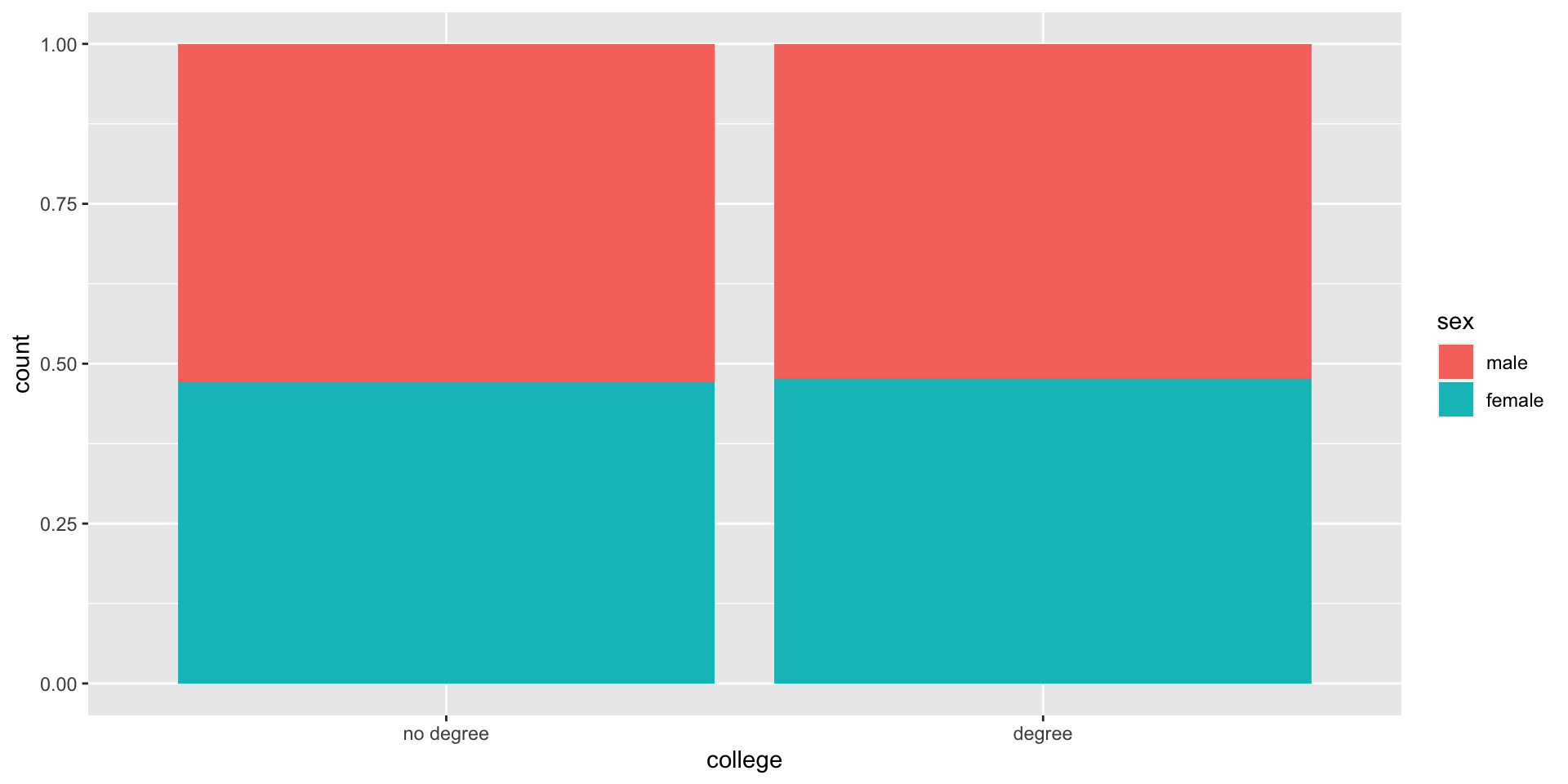
Bar charts for two categorical variables

Example: How is the probability of obtaining a college degree related to self-identified income category?

table(gss$college, gss$finrela)

           
            far below average below average average above average
  no degree                21            81     165            52
  degree                    4            34      74            54
           
            far above average  DK
  no degree                 2   5
  degree                    8   0

Bar charts for two categorical vars

Example: How is the probability of obtaining a college degree related to self-identified income category?
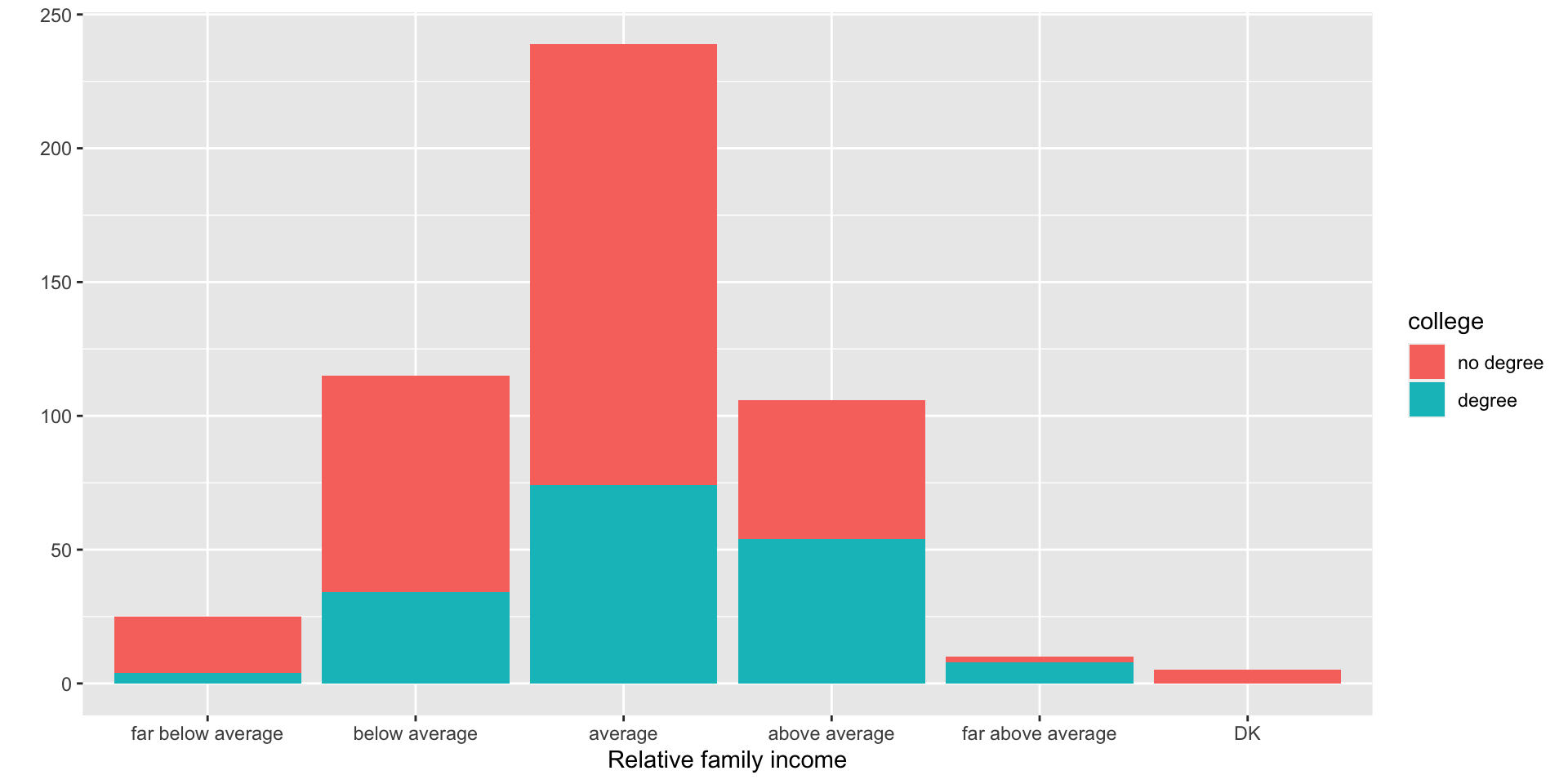
Stacked bar chart: Good at showing the overall distribution. We can see that most people think their income is average.

ggplot(gss, 
       aes(x = finrela, fill = college)) + 
  geom_bar() + 
  labs(x = "Relative family income",
       y = "")

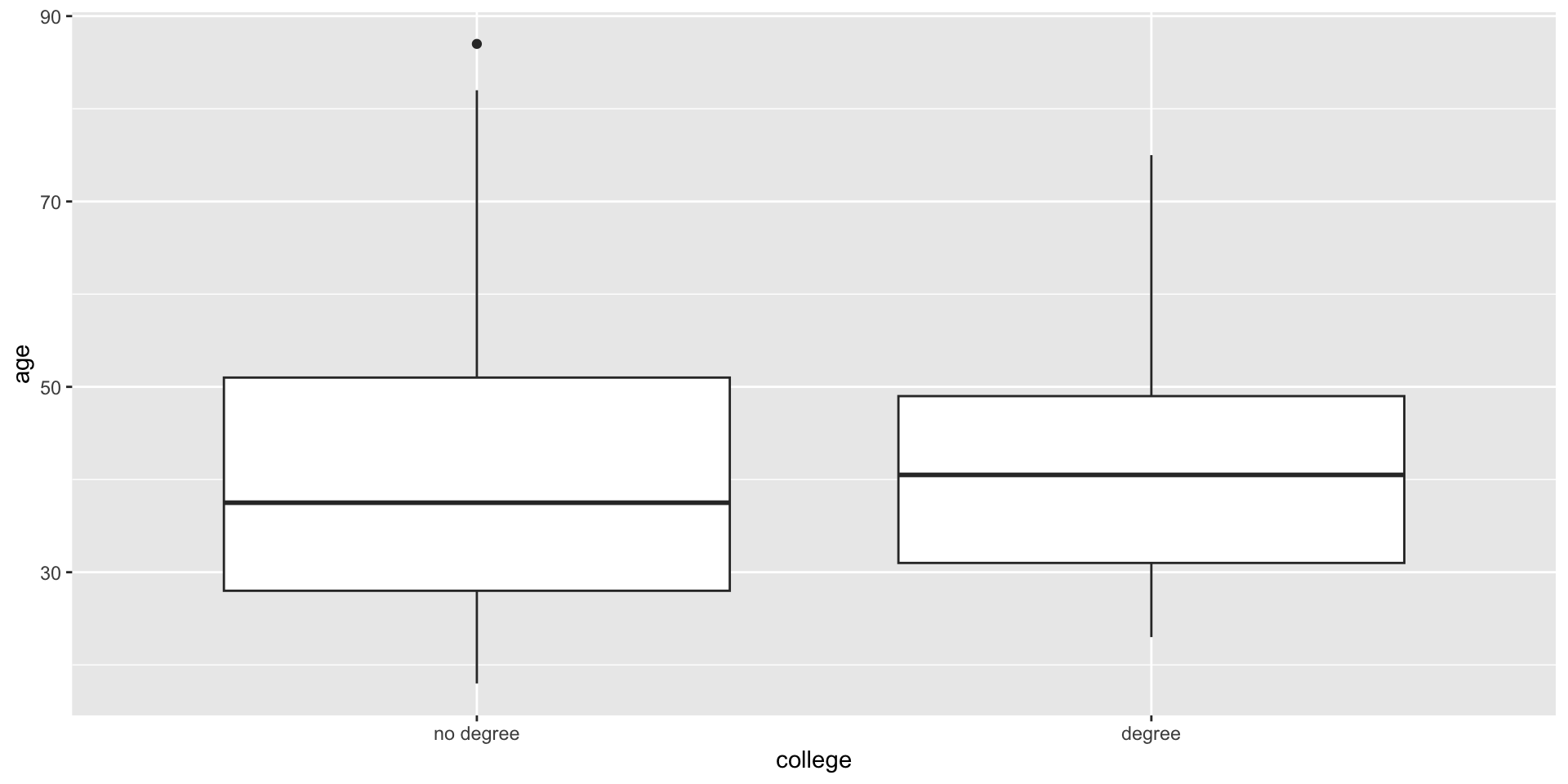
Bar charts for two categorical vars

Example: How is the probability of obtaining a college degree related to self-identified income category?

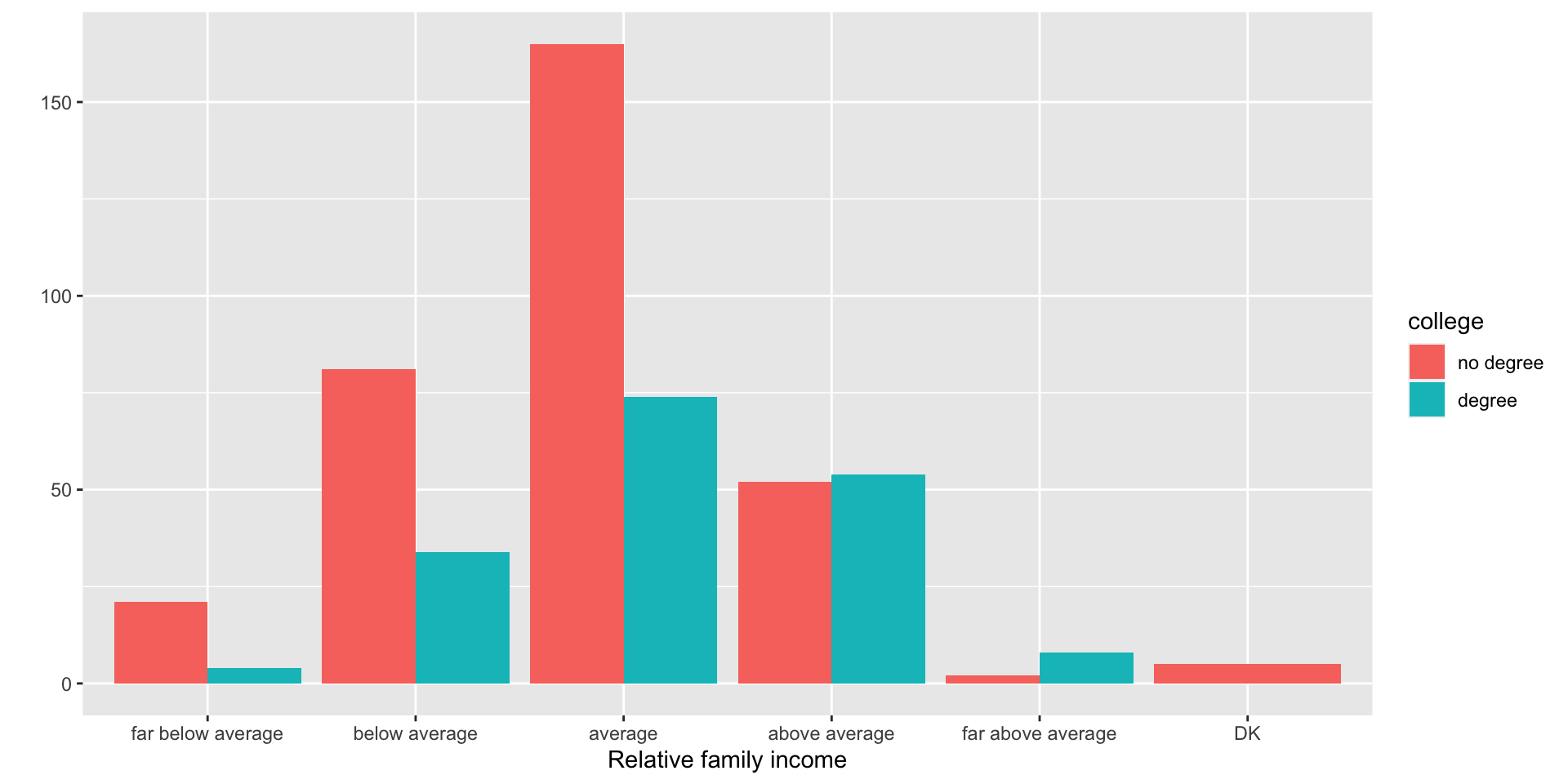
Dodged bar chart: Good at showing the distributions of the two groups next to each other. Now we can see that there are fewer people with degrees.

ggplot(gss, 
       aes(x = finrela, fill = college)) + 
  # the "position" argument here 
  # is what is changing
  geom_bar(position = "dodge") +
  labs(x = "Relative family income",
       y = "")

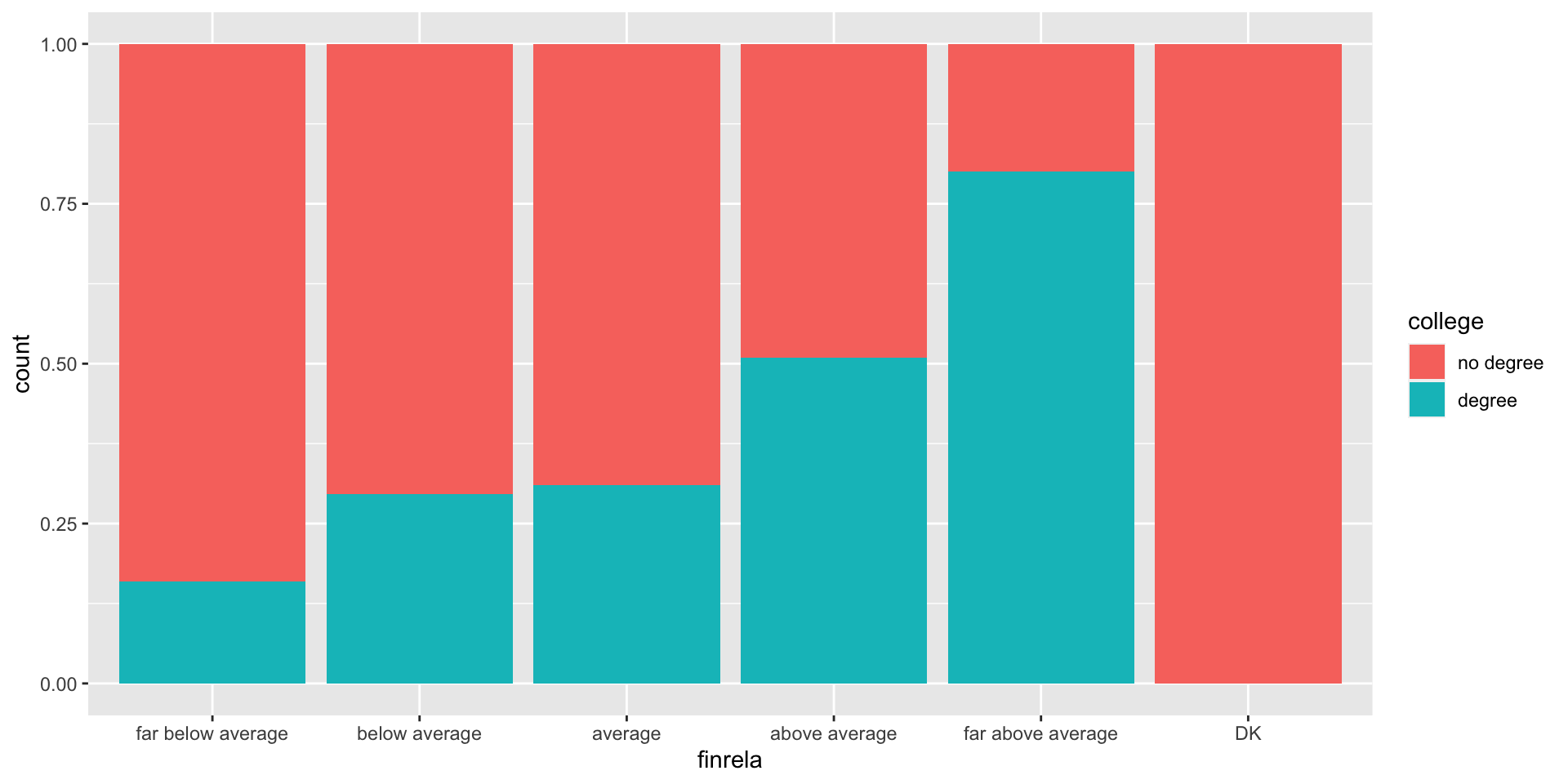
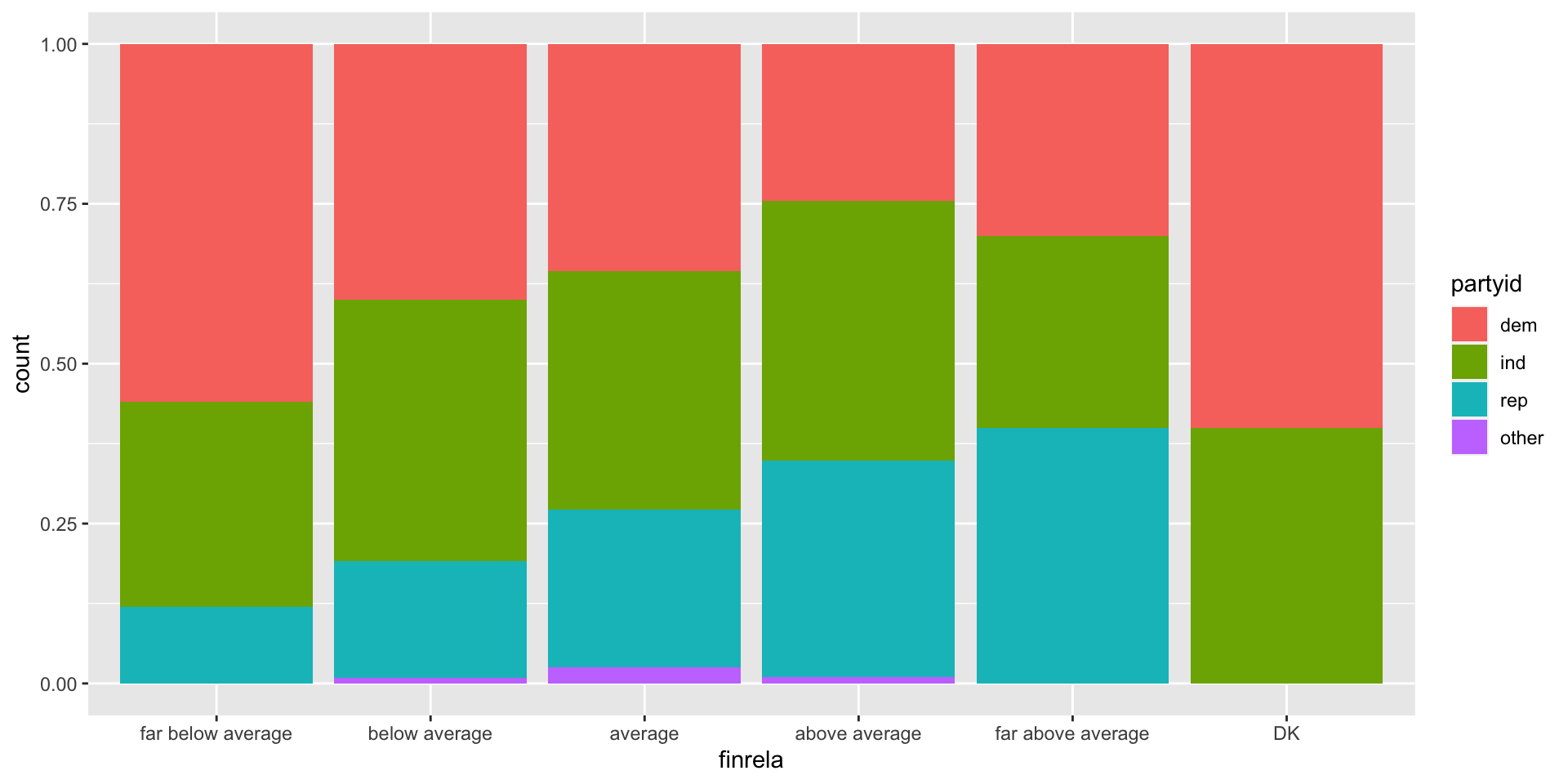
Bar charts for two categorical vars

Example: How is the probability of obtaining a college degree related to self-identified income category?

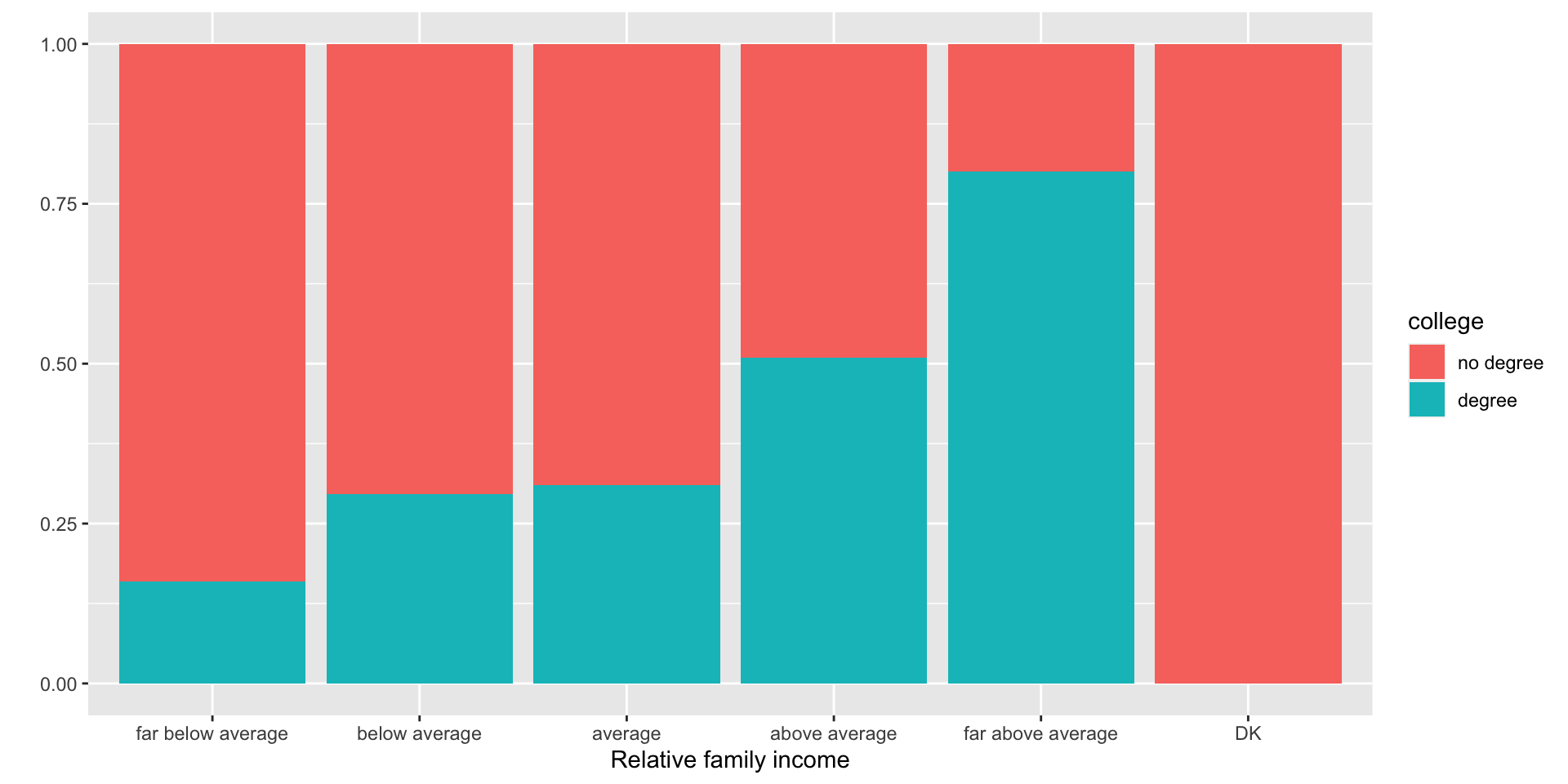
Proportion bar chart: Good at comparing the compositions of the bars. We lose information on the distribution as a whole, but we gain information on whether people from both groups are evenly distributed between income classes.

ggplot(gss, 
       aes(x = finrela, fill = college)) + 
  # the "position" argument here 
  # is what is changing
  geom_bar(position = "fill") +
  labs(x = "Relative family income",
       y = "")

Answers for exercise Q3

How is someone’s gender identity related to their probability of being married?

Where we’re at with hypothesis testing

There are many types of tests

But the steps to run them are the same

Calculate the test statistic of your sample
- with specify() (telling R what your variables are),
- then hypothesize() (telling R what kind of null hypothesis you have),
- then calculate() (calculating your test statistic)
Simulate the null distribution
- exactly the same code as step 1, but with an added generate() step
- here you are simulating pulling a bunch of samples from your null population in order to figure out what the null distribution of sample statistics would look like
Calculate the p value of your sample
- with your null distribution, your test statistic, and get_p_value()
Visualize the test statistic of your sample alongside the null distribution
- with visualize() and shade_p_value()

In code form:

# 1. Calculate test statistic
test_stat <- XXXX |> 
  specify(explanatory = XXXX,
          response = XXXX) |> 
  hypothesize(null = "independence") |> 
  calculate(stat = XXXX)

# 2. Simulate null distribution
null_dist <- XXXX |> 
  specify(explanatory = XXXX,
          response = XXXX) |> 
  hypothesize(null = "independence") |>
  generate(reps = 1000) |>
  calculate(stat = XXXX)

# 3. Use both to get the p value
get_p_value(null_dist,
            obs_stat = test_stat,
            direction = XXXX)

# 4. Visualize it!
visualize(null_dist) +
  shade_p_value(obs_stat = test_stat,
                direction = XXXX)

What are the different tests testing?

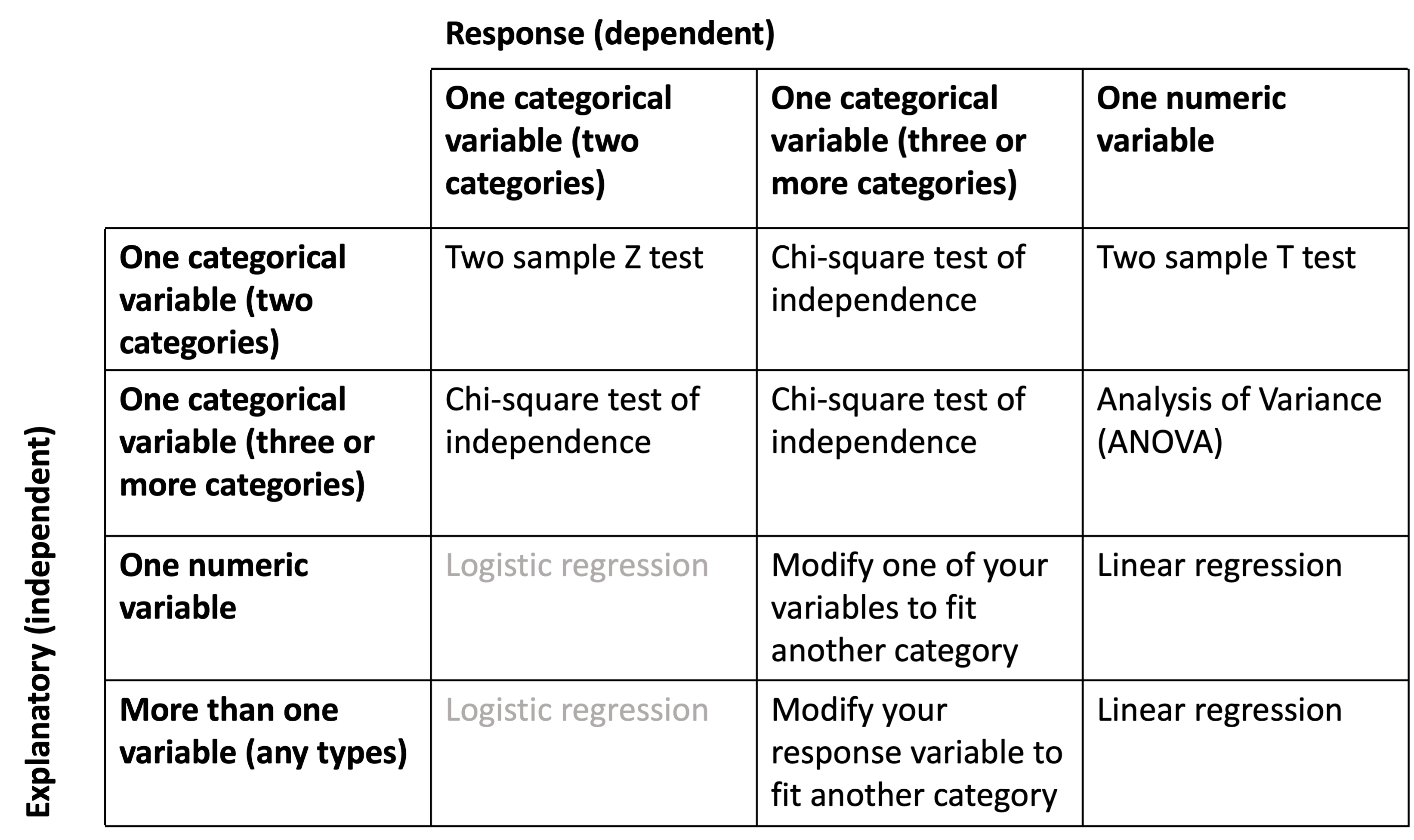
Different tests: an overview

We’ll be covering 5 specific hypothesis tests (all except logistic regression)
- Two sample Z test
- Two sample T test
- Chi square test of independence
- Analysis of Variance (ANOVA)
- Linear regression

There is a relationship between the descriptive plots you’ve been working with and the different test types!

Two sample Z test

Explanatory: categorical with two categories
Response: categorical with two categories
Testing for: Difference in group proportions!

Two sample T test

Explanatory: categorical with two categories
Response: numeric
Testing for: Difference in group means!

Chi square test of independence

Explanatory: categorical with any number of categories
Response: categorical with any number of categories
Testing for: Patterns in how observations are distributed between groups!

Chi square test of independence

Explanatory: categorical with any number of categories
Response: categorical with any number of categories
Testing for: Patterns in how observations are distributed between groups!

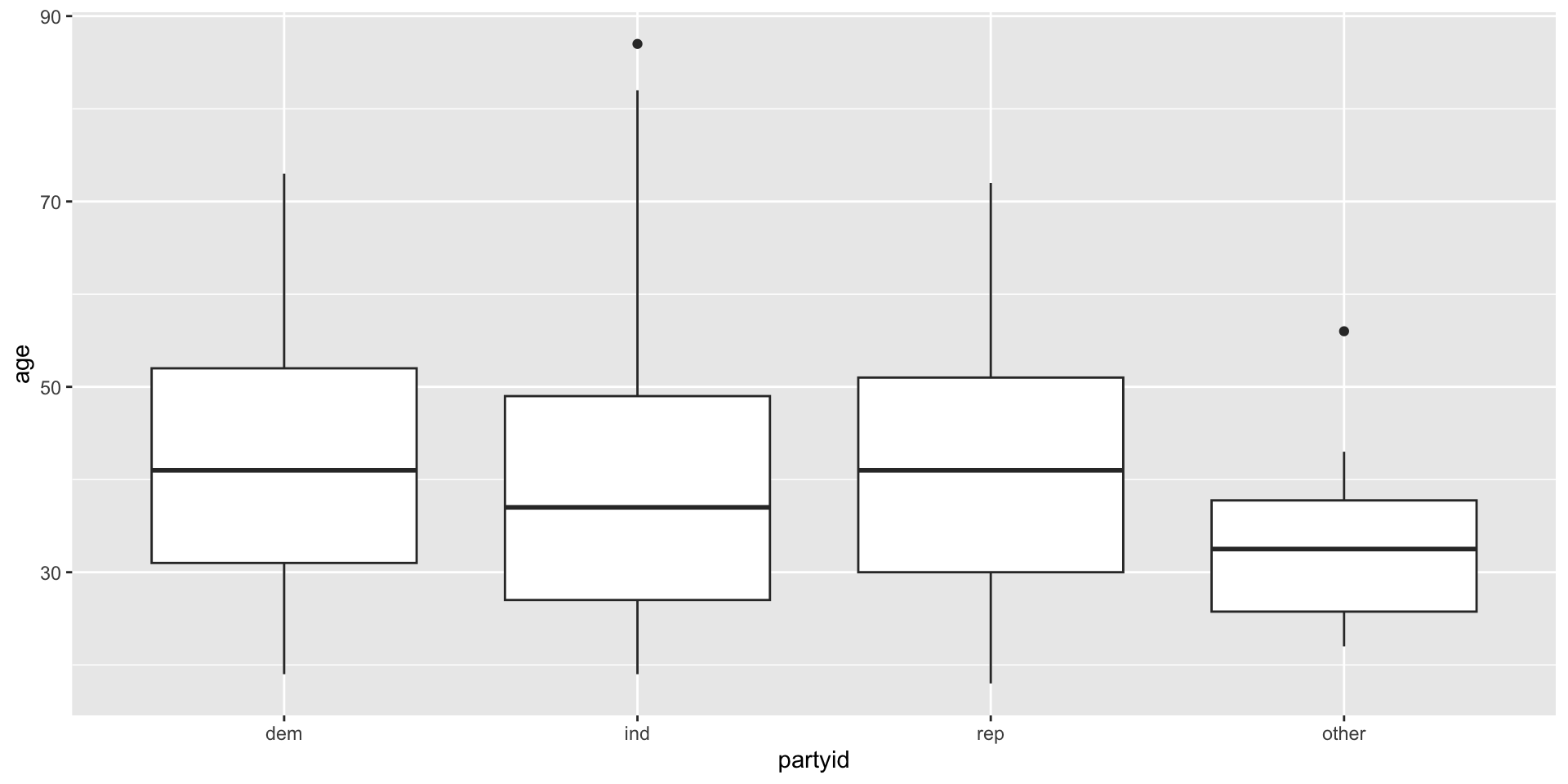
Analysis of Variance (ANOVA)

Explanatory: categorical with three or more categories
Response: numeric
Testing for: Differences in means between more groups!

Linear regression

Explanatory: numeric or multiple variables
Response: numeric
Testing for: Non-zero slopes!

What’s the math difference?

Mainly, the shape of the test statistic distribution.
We account for this in two places:
- the stat argument in calculate()
- the direction argument in get_p_value() and visualize()

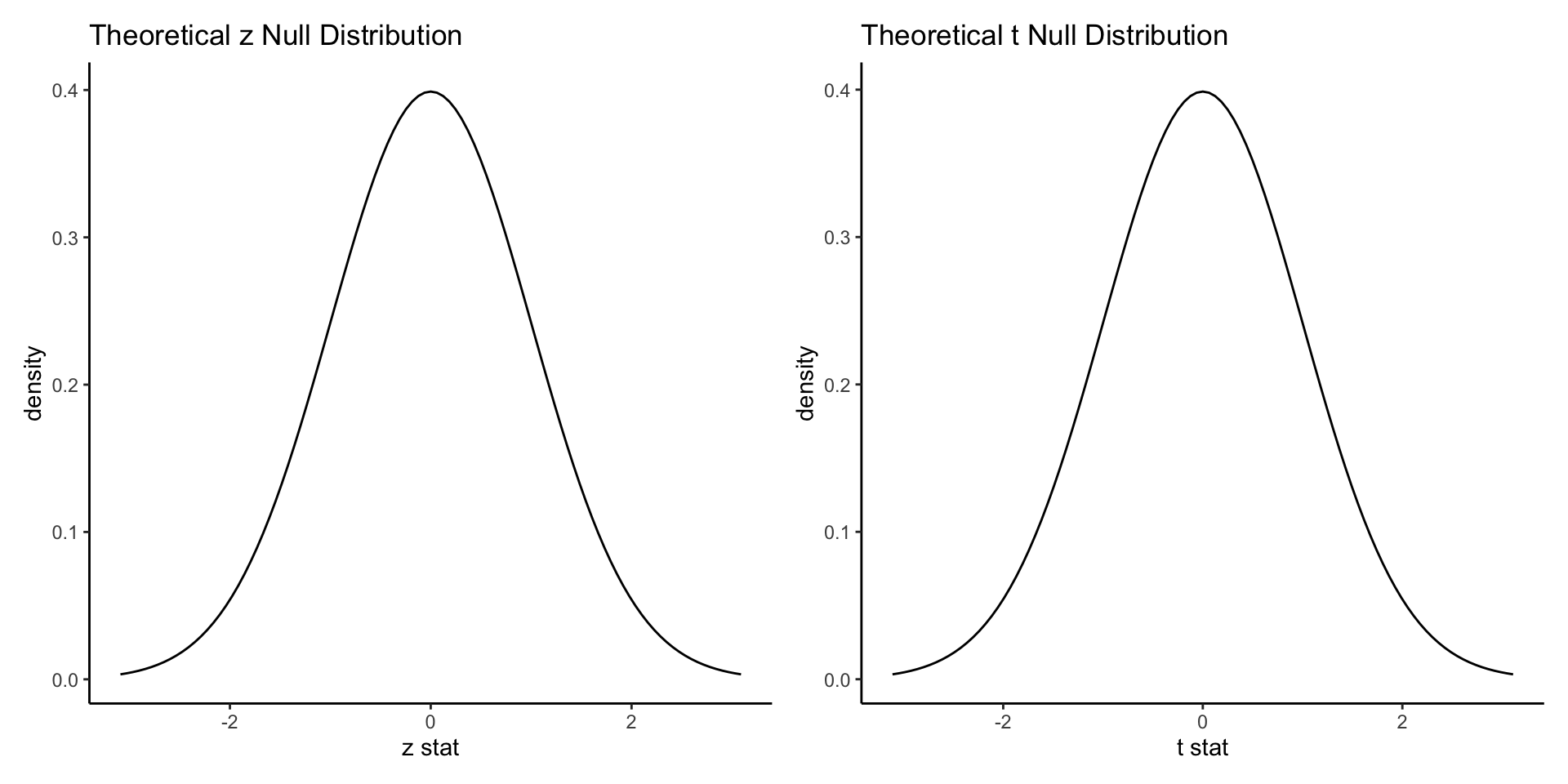
Normal and nearly normal distributions

Normal: Two sample Z test, linear regression slope test
Nearly normal (t distribution): Two sample T test
Symmetrical; centered at 0; bell-shaped
Either one-tailed or two-tailed tests make sense

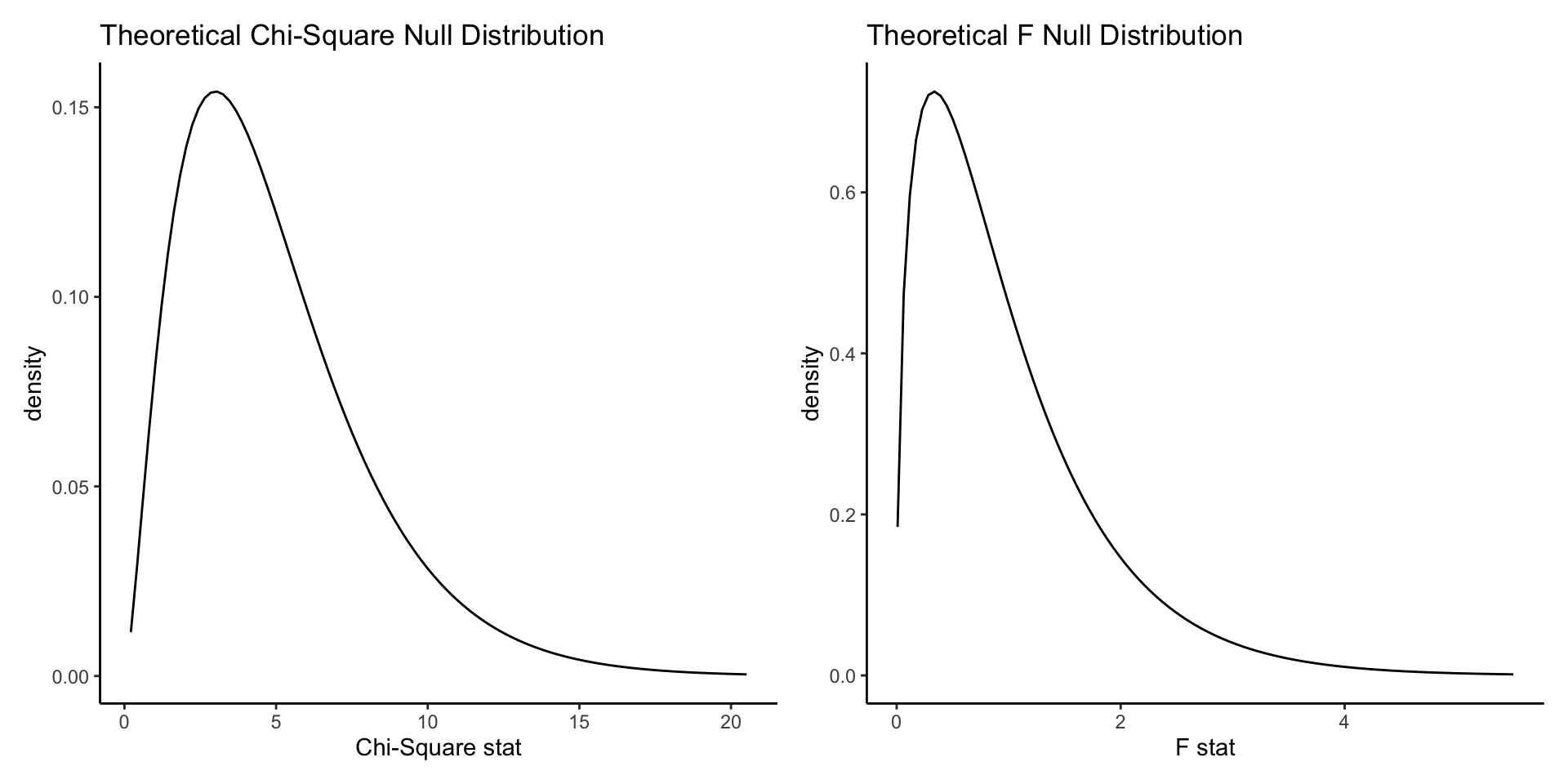
Asymmetrical distributions

Chi-square test: chi square distribution
Analysis of Variance (ANOVA): F distribution
These values can be thought of as distances
Strictly positive; asymmetrical and long-tailed
“More extreme” means further away—ie, more positive. So all tests are one-tailed.

Different tests: summary

Test	stat = XXXX	direction = XXXX	Notes
Two sample Z test	`"z"`	usually `"two-sided"`	Needs `success = XXXX` in `specify()`, where XXXX is one of the options of the response variable
Two sample T test	`"t"`	usually `"two-sided"`
Chi square test	`"Chisq"`	`"greater"`
ANOVA	`"F"`	`"greater"`	`hypothesize()` optional for test statistic
Linear regression	`"slope"`	usually `"two-sided"`	`hypothesize()` optional for test statistic

Example

How is self-perceived relative family income associated with probability of receiving a college degree?

Explanatory: Self-perceived relative family income. Three or more category categorical.
Response: Whether or not someone received a college degree. Two-category categorical.

Null hypothesis: There is no relationship between self-perceived relative family income and probability of receiving a college degree.
Alternative hypothesis: There is no relationship between self-perceived relative family income and probability of receiving a college degree.

Example

ggplot(gss, aes(x = finrela, fill = college)) + 
  geom_bar(position = "fill")

Chi square example

Correct test: Chi square

Chi square example

# 1. Calculate test statistic
test_stat <- gss |> 
  specify(explanatory = finrela,
          response = college) |> 
  hypothesize(null = "independence") |> 
  calculate(stat = "Chisq")       # calculate the Chi square statistic

Chi square example

# 1. Calculate test statistic
test_stat <- gss |> 
  specify(explanatory = finrela,
          response = college) |> 
  hypothesize(null = "independence") |> 
  calculate(stat = "Chisq")       # calculate the Chi square statistic

# 2. Simulate null distribution
null_dist <- gss |> 
  specify(explanatory = finrela,
          response = college) |> 
  hypothesize(null = "independence") |>
  generate(reps = 1000) |>
  calculate(stat = "Chisq")

Chi square example

# 1. Calculate test statistic
test_stat <- gss |> 
  specify(explanatory = finrela,
          response = college) |> 
  hypothesize(null = "independence") |> 
  calculate(stat = "Chisq")       # calculate the Chi square statistic

# 2. Simulate null distribution
null_dist <- gss |> 
  specify(explanatory = finrela,
          response = college) |> 
  hypothesize(null = "independence") |>
  generate(reps = 1000) |>
  calculate(stat = "Chisq")

# 3. Use both to get the p value
get_p_value(null_dist,
            obs_stat = test_stat,
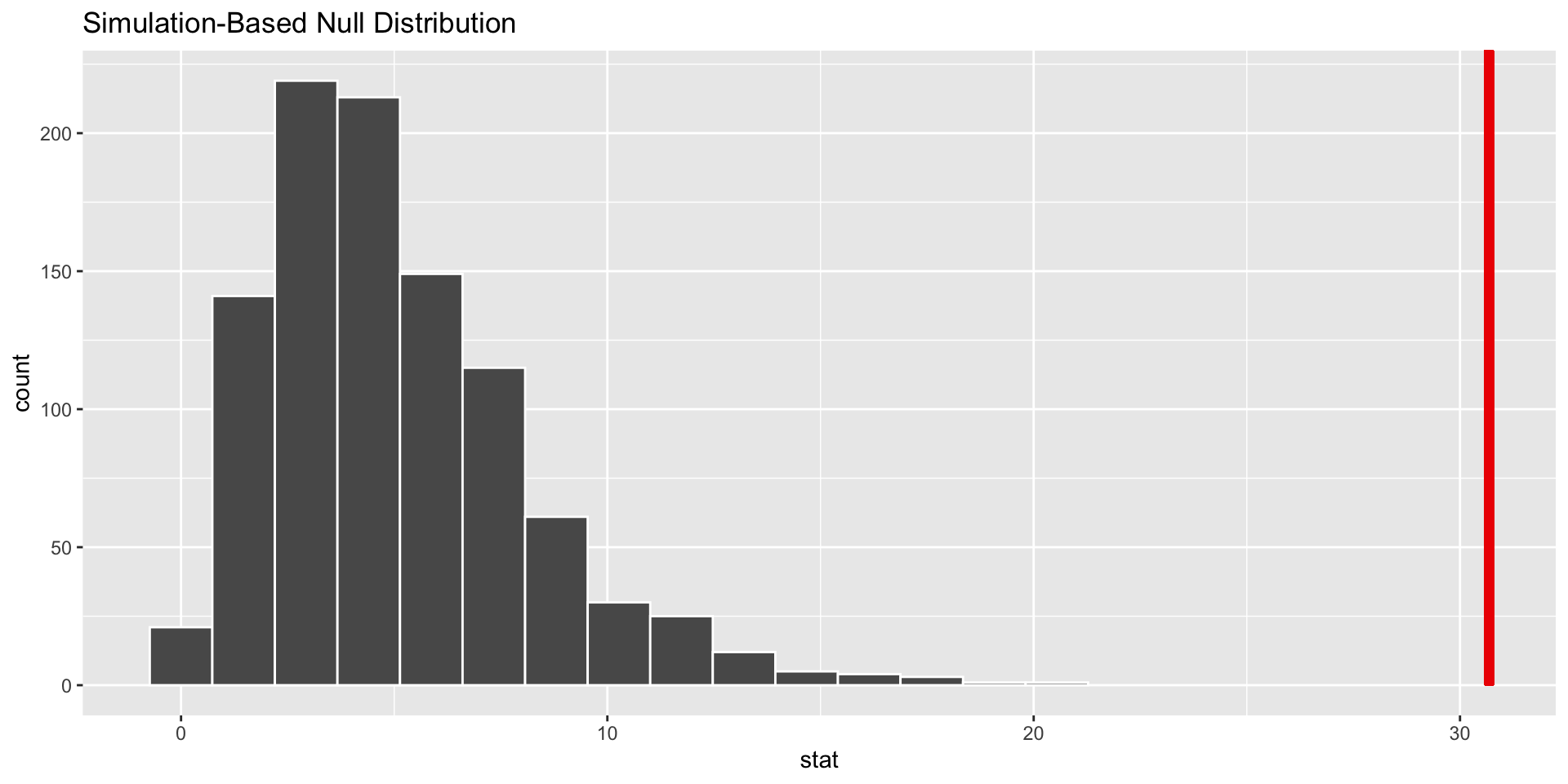
            direction = "greater") # we want the probability of a statistic larger than what we calculated

# A tibble: 1 × 1
  p_value
    <dbl>
1       0

Chi square example

Do we reject or fail to reject our null hypothesis?
What can we conclude about our research question?

# 4. Visualize it!
visualize(null_dist) +
  shade_p_value(obs_stat = test_stat,
                direction = "greater")